Suppose the graph of (x,y) is first almost linear, then relatively flat, then almost linear again. How to find the middle flat regime?
# diff1 saves the difference of current value and predicted value using existing points from the left side
k<-length(x)
diff1<-c()
for(i in c(2:k)) {
tx<-x[1:i]
ty<-y[1:i]
tfitted<-glm(ty ~ tx)
diff1<-c(diff1, residuals(tfitted)[i])
}
diff1<-c(diff1[1],diff1)
# diff2 saves the difference of current value and predicted value using existing points from the right side
diff2<-c()
for(i in c((k-1):1)) {
tx<-x[i:k]
ty<-y[i:k]
tfitted<-glm(ty ~ tx)
diff2<-c(residuals(tfitted)[1], diff2)
}
diff2<-c(diff2,diff2[k-1])
Showing posts with label R. Show all posts
Showing posts with label R. Show all posts
Tuesday, March 29, 2011
Monday, March 28, 2011
How to plot curvature in R
tmp<-read.table("tmp.txt")
x<-tmp[,1]
y<-tmp[,2]
f<-y
# find 1st derivative using forward difference
k<-length(x)
y1<-c()
for(i in c(1:k-1)) {
t<-(y[i+1]-y[i])/(x[i+1]-x[i])
y1<-c(y1, t)
}
y1<-c(y1,t)
f1<-y1
# find 2nd derivative using backward difference of 1st derivative
y<-f1
y1<-c()
for(i in c(2:k)) {
t<-(y[i]-y[i-1])/(x[i]-x[i-1])
y1<-c(y1, t)
}
y1<-c(y1[1],y1)
f2<-y1
# find curvature and plot
kappa<-f2/(1+f1*f1)^1.5
plot(x,kappa)
-------------------------------------------------------------------------
We can also use the backward difference to approximate the 1st derivative:
tmp<-read.table("tmp.txt")
x<-tmp[,1]
y<-tmp[,2]
f<-y
# find 1st derivative using backward difference
k<-length(x)
y1<-c()
for(i in c(2:k)) {
t<-(y[i]-y[i-1])/(x[i]-x[i-1])
y1<-c(y1, t)
}
y1<-c(y1[1],y1)
f1<-y1
# find 2nd derivative using forward difference of 1st derivative
y<-f1
y1<-c()
for(i in c(1:k-1)) {
t<-(y[i+1]-y[i])/(x[i+1]-x[i])
y1<-c(y1, t)
}
y1<-c(y1,t)
f2<-y1
# find curvature and plot
kappa<-f2/(1+f1*f1)^1.5
plot(x,kappa)
-------------------------------------------------------------------------
Finally, we can use central difference to approximate both the 1st and 2nd derivative. Here we assume the mesh grid is uniform.
tmp<-read.table("tmp.txt")
x<-tmp[,1]
y<-tmp[,2]
f<-y
# find 1st derivative using central difference
k<-length(x)
y1<-c()
for(i in c(2:k-1)) {
t<-(y[i+1]-y[i-1])/(x[i+1]-x[i-1])
y1<-c(y1, t)
}
y1<-c(y1,t)
y1<-c(y1[1],y1)
f1<-y1
# find 2nd derivative using central difference
y<-f1
y1<-c()
for(i in c(2:k-1)) {
t<-(y[i+1]-2*y[i]+y[i-1])/(x[i+1]-x[i])^2
y1<-c(y1, t)
}
y1<-c(y1,t)
y1<-c(y1[1],y1)
f2<-y1
# find curvature and plot
kappa<-f2/(1+f1*f1)^1.5
plot(x,kappa)
x<-tmp[,1]
y<-tmp[,2]
f<-y
# find 1st derivative using forward difference
k<-length(x)
y1<-c()
for(i in c(1:k-1)) {
t<-(y[i+1]-y[i])/(x[i+1]-x[i])
y1<-c(y1, t)
}
y1<-c(y1,t)
f1<-y1
# find 2nd derivative using backward difference of 1st derivative
y<-f1
y1<-c()
for(i in c(2:k)) {
t<-(y[i]-y[i-1])/(x[i]-x[i-1])
y1<-c(y1, t)
}
y1<-c(y1[1],y1)
f2<-y1
# find curvature and plot
kappa<-f2/(1+f1*f1)^1.5
plot(x,kappa)
-------------------------------------------------------------------------
We can also use the backward difference to approximate the 1st derivative:
tmp<-read.table("tmp.txt")
x<-tmp[,1]
y<-tmp[,2]
f<-y
# find 1st derivative using backward difference
k<-length(x)
y1<-c()
for(i in c(2:k)) {
t<-(y[i]-y[i-1])/(x[i]-x[i-1])
y1<-c(y1, t)
}
y1<-c(y1[1],y1)
f1<-y1
# find 2nd derivative using forward difference of 1st derivative
y<-f1
y1<-c()
for(i in c(1:k-1)) {
t<-(y[i+1]-y[i])/(x[i+1]-x[i])
y1<-c(y1, t)
}
y1<-c(y1,t)
f2<-y1
# find curvature and plot
kappa<-f2/(1+f1*f1)^1.5
plot(x,kappa)
-------------------------------------------------------------------------
Finally, we can use central difference to approximate both the 1st and 2nd derivative. Here we assume the mesh grid is uniform.
tmp<-read.table("tmp.txt")
x<-tmp[,1]
y<-tmp[,2]
f<-y
# find 1st derivative using central difference
k<-length(x)
y1<-c()
for(i in c(2:k-1)) {
t<-(y[i+1]-y[i-1])/(x[i+1]-x[i-1])
y1<-c(y1, t)
}
y1<-c(y1,t)
y1<-c(y1[1],y1)
f1<-y1
# find 2nd derivative using central difference
y<-f1
y1<-c()
for(i in c(2:k-1)) {
t<-(y[i+1]-2*y[i]+y[i-1])/(x[i+1]-x[i])^2
y1<-c(y1, t)
}
y1<-c(y1,t)
y1<-c(y1[1],y1)
f2<-y1
# find curvature and plot
kappa<-f2/(1+f1*f1)^1.5
plot(x,kappa)
Wednesday, March 23, 2011
How to find the least dense part of a curve in R
Suppose we have vectors x and y of same size. Then we plotted x vs. y using plot(x,y) in R. How to find the least dense part of this curve?
k<-length(x)
a<-c()
for(i in c(1:k-1)) {
t<-sqrt((x[i+1]-x[i])^2+(y[i+1]-y[i])^2)
a<-c(a, t)
}
a<-c(a, t)
plot(x,a)
k<-length(x)
a<-c()
for(i in c(1:k-1)) {
t<-sqrt((x[i+1]-x[i])^2+(y[i+1]-y[i])^2)
a<-c(a, t)
}
a<-c(a, t)
plot(x,a)
Friday, March 11, 2011
How to find minimizer in R
Suppose x is a vector, the following command finds its minimum:
min(x)
To find the minimizer, we can use the following command:
which(x==min(x))
It gives the index for the minimum.
min(x)
To find the minimizer, we can use the following command:
which(x==min(x))
It gives the index for the minimum.
How to plot derivative in R
Suppose we have two lists x and y of equal size, and we want to plot x vs y1=dy/dx. How to do this in R?
M<-read.table("tmp.txt")
x<-M[,1]
y<-M[,2]
k<-length(x)
y1<-c()
for(i in c(1:k-1)) {
t<-(y[i+1]-y[i])/(x[i+1]-x[i])
y1<-c(y1, t)
}
y1<-c(y1, t)
plot(x,y1)
M<-read.table("tmp.txt")
x<-M[,1]
y<-M[,2]
k<-length(x)
y1<-c()
for(i in c(1:k-1)) {
t<-(y[i+1]-y[i])/(x[i+1]-x[i])
y1<-c(y1, t)
}
y1<-c(y1, t)
plot(x,y1)
Friday, February 25, 2011
How to color points by variable in R
Suppose we wan to plot x vs y according to the sign of z: if z > 0, we plot blue, while if z < 0, we plot red.
(1) Find the color code for "red" and "blue".
> grep("red",colors())
[1] 100 372 373 374 375 376 476 503 504 505 506 507 524 525 526 527 528 552 553 [20] 554 555 556 641 642 643 644 645
> grep("blue",colors())
[1] 2 26 27 28 29 30 31 42 43 44 45 46 62 73 107 121 122 123 124 [20] 125 128 129 130 131 132 399 400 401 402 403 430 431 432 433 434 435 438 439 [39] 440 441 442 461 473 477 491 546 562 563 564 565 566 589 590 591 592 593 594 [58] 595 596 597 598 615 616 617 618 619
(2) Generate our color vector.
> mycol<-563-(563-552)*(1-(sign(z)+1)/2)
(3) Plot using the color vector.
> plot(x, y, col=colors()[mycol])
(1) Find the color code for "red" and "blue".
> grep("red",colors())
[1] 100 372 373 374 375 376 476 503 504 505 506 507 524 525 526 527 528 552 553 [20] 554 555 556 641 642 643 644 645
> grep("blue",colors())
[1] 2 26 27 28 29 30 31 42 43 44 45 46 62 73 107 121 122 123 124 [20] 125 128 129 130 131 132 399 400 401 402 403 430 431 432 433 434 435 438 439 [39] 440 441 442 461 473 477 491 546 562 563 564 565 566 589 590 591 592 593 594 [58] 595 596 597 598 615 616 617 618 619
(2) Generate our color vector.
> mycol<-563-(563-552)*(1-(sign(z)+1)/2)
(3) Plot using the color vector.
> plot(x, y, col=colors()[mycol])
Thursday, January 20, 2011
How to produce a double-well graph in R
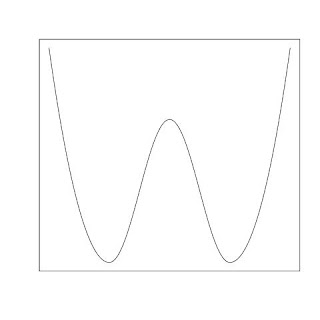To create a double-well image as the one in the above, we can do it in three steps(1) The left of the first bottom can use the graph of a parabolic function.
(2) From the first bottom to the second bottom can use the graph of a cosine function.
(3) The right of the second bottom can use the graph of another parabolic function.
The following R code generates the graph above:
x2<-c(0:100)*0.02+1
y2<-cos((x2-2)*pi)
x1<-c(0:100)*0.01
y1<-3*(x1-1)^2
x3<-c(0:100)*0.01+3
y3<-3*(x3-3)^2
jpeg("doublewell.jpg")
plot(x2,y2,xlim=c(0,4),ylim=c(0,3),'l',xlab="",ylab="",xaxt="n",yaxt="n")
lines(x1,y1)
lines(x3,y3)
dev.off()
Thursday, April 22, 2010
How I used R to create a new world university ranking
This website gives the 2010 world university ranking in the "Engineering and IT" category. I would like to see the ranking ordered by "Citations per Paper", as I felt that it tells more about the quality of the research in that university.
So I first copied the results from that website, save it to a txt file called "worldIT.txt". Then I used vim to add quotation marks around university and country names. Then I imported the file into R, and did the sorting as the following:
worldIT<-read.table("worldIT.txt")
worldIT.sorted<-worldIT[with(worldIT,order(worldIT$V5,decreasing=TRUE)),]
r<-c(1:100)
worldITnew<-cbind(r,worldIT.sorted)
worldITnew[,c("r","V2","V3","V5")]
This gives me the following ranking:
Rank Name Country Citations per Paper
1 Harvard University United States 4.8
2 California Institute of Technology (Caltech) United States 4.6
3 University of California, Berkeley United States 4.5
4 Princeton University United States 4.4
5 Massachusetts Institute of Technology (MIT) United States 4.2
6 Stanford University United States 4.2
7 University of California, Los Angeles (UCLA) United States 4.2
8 University of California, Santa Barbara United States 4.2
9 University of Pennsylvania United States 3.9
10 University of Washington United States 3.9
11 Cornell University United States 3.7
12 Yale University United States 3.7
13 Johns Hopkins University United States 3.6
14 ETH Zurich (Swiss Federal Institute of Technology) Switzerland 3.5
15 Columbia University United States 3.5
16 Brown University United States 3.5
17 University of Toronto Canada 3.4
18 University of Cambridge United Kingdom 3.3
19 University of Michigan United States 3.3
20 Carnegie Mellon University United States 3.1
21 ¨|cole Polytechnique F¨|d¨|rale de Lausanne Switzerland 3.1
22 University of Wisconsin-Madison United States 3.1
23 University of Oxford United Kingdom 3.0
24 University of California, San Diego United States 3.0
25 UCL (University College London) United Kingdom 3.0
26 Ecole Normale Sup¨|rieure, Paris France 3.0
27 Georgia Institute of Technology United States 2.9
28 National University of Singapore (NUS) Singapore 2.9
29 University of British Columbia Canada 2.9
30 University of Illinois, Urbana-Champaign United States 2.9
31 University of Texas at Austin United States 2.9
32 Pohang University of Science and Technology (POSTECH) Korea, South 2.9
33 Technical University of Denmark Denmark 2.9
34 Pennsylvania State University United States 2.9
35 University of Hong Kong Hong Kong 2.8
36 Rensselaer Polytechnic Institute United States 2.8
37 City University of Hong Kong Hong Kong 2.8
38 University of Bristol United Kingdom 2.8
39 Imperial College London United Kingdom 2.7
40 Hong Kong University of Science and Technology Hong Kong 2.7
41 Katholieke Universiteit Leuven Belgium 2.7
42 McMaster University Canada 2.7
43 University of Melbourne Australia 2.6
44 University of Manchester United Kingdom 2.6
45 Eindhoven University of Technology Netherlands 2.6
46 University of Birmingham United Kingdom 2.6
47 Purdue University United States 2.5
48 University of Alberta Canada 2.5
49 University of Queensland Australia 2.5
50 Technion - Israel Institute of Technology Israel 2.4
51 ¨|cole Polytechnique France 2.4
52 Australian National University Australia 2.4
53 Technische Universit?t M¨1nchen Germany 2.4
54 University of Southampton United Kingdom 2.4
55 McGill University Canada 2.3
56 University of Edinburgh United Kingdom 2.3
57 Chalmers University of Technology Sweden 2.3
58 Delft University of Technology Netherlands 2.2
59 Seoul National University Korea, South 2.2
60 Nanyang Technological University (NTU) Singapore 2.2
61 Virginia Polytechnic Institute (Virginia Tech) United States 2.2
62 The Chinese University of Hong Kong Hong Kong 2.2
63 KAIST - Korea Advanced Institute of Science & Technology Korea, South 2.1
64 University of Waterloo Canada 2.1
65 University of New South Wales Australia 2.1
66 National Taiwan University Taiwan 2.1
67 Monash University Australia 2.1
68 KTH, Royal Institute of Technology Sweden 2.1
69 Texas A&M University United States 2.1
70 Universit?t Stuttgart Germany 2.1
71 The Hong Kong Polytechnic University Hong Kong 2.1
72 University of Sydney Australia 2.0
73 Rheinisch-Westf?lische Technische Hochschule Aachen Germany 2.0
74 Tohoku University Japan 2.0
75 National Tsing Hua University Taiwan 2.0
76 University of Tokyo Japan 1.9
77 Kyoto University Japan 1.9
78 Indian Institute of Technology Bombay (IITB) India 1.9
79 Indian Institute of Technology Delhi (IITD) India 1.9
80 Indian Institute of Technology Kanpur (IITK) India 1.9
81 Technische Universit?t Berlin Germany 1.9
82 Universit?t Karlsruhe Germany 1.9
83 Helsinki University of Technology TKK Finland 1.9
84 Tokyo Institute of Technology Japan 1.8
85 Politecnico di Milano Italy 1.8
86 Vienna University of Technology Austria 1.8
87 Chulalongkorn University Thailand 1.8
88 Osaka University Japan 1.7
89 The University of Auckland New Zealand 1.7
90 Indian Institute of Technology Madras (IITM) India 1.7
91 Indian Institute of Technology Kharagpur (IITKGP) India 1.7
92 Fudan University China 1.7
93 University of Calgary Canada 1.7
94 Peking University China 1.6
95 University of Science and Technology of China China 1.6
96 Nagoya University Japan 1.6
97 RMIT University Australia 1.4
98 Tsinghua University China 1.2
99 Shanghai Jiao Tong University China 1.1
100 Bandung Institute of Technology (ITB) Indonesia 0.6
Subscribe to:
Posts (Atom)
